今天我們來解釋昨天介紹的「吾乃數論學家」為何是晶格密碼學？
與之前的二維晶格相似，關鍵都在解碼的正確性

回顧解碼正確性的證明

之所以解碼會成功，主要原因是因為

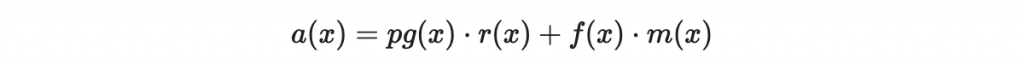
之右手邊部分的係數可以被控制，所以我們可以還原出整數上的等號（非模除上的等號），然後再做後續的有號提升與模除 p 運算。

意思是，如果我們想要偽造一個假的密鑰 (f(x), g(x)) ，那他只要滿足

一、

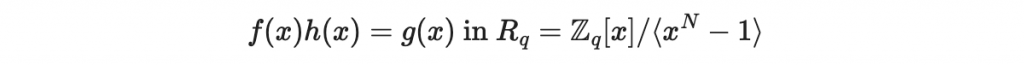
其中 h(x) 與 q 是公鑰的內容。

二、f(x) 與 g(x) 的係數都不大，以至於以下多項式的係數絕對值不超過 q/2。

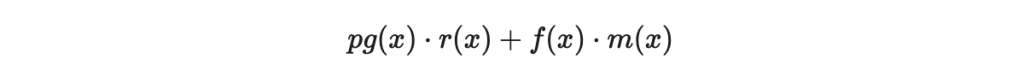
這個步驟是不是與之前看到的二維晶格非常雷同？😀

將多項式乘法寫為矩陣乘法

為了要用向量空間討論，我們應該介紹一個用矩陣乘法來寫的多項式乘法：

考慮在 R 底下的運算

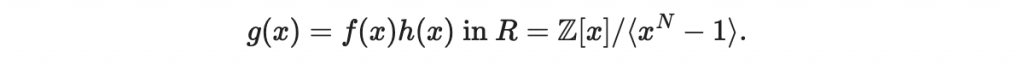
並將係數寫好

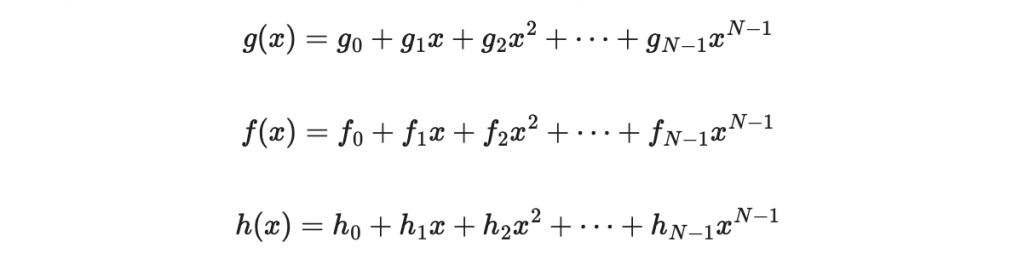
（以下的數學看過即可，我們會用程式驗證）
那麼根據在 R 底下的模除運算規則，我們知道

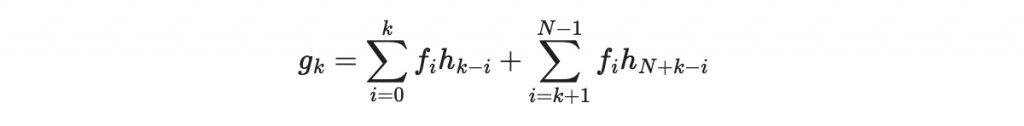
為了進一步分析，我們將其寫成矩陣形式：

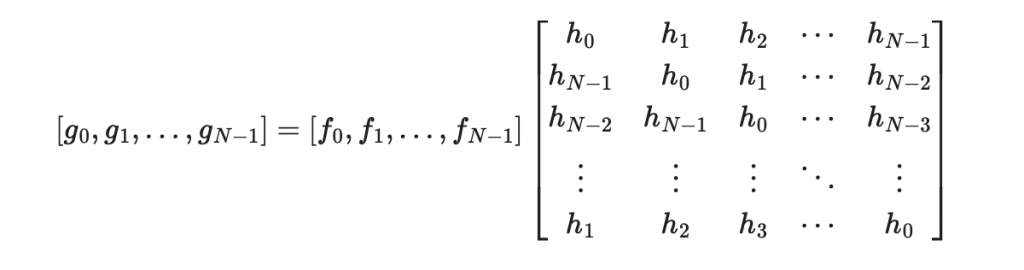
簡寫為：

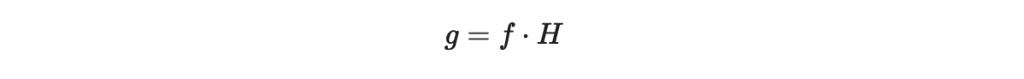
好，證明部分很無聊，我們用程式簡單驗證看看：

N = 11

# 多項式環
R_poly = quotient(PolynomialRing(ZZ,x),x^N-1)

# 隨機生成多項式
f = R_poly([randint(-10,10) for i in range(N)])
h = R_poly([randint(-10,10) for i in range(N)])

print("f =", f)
print("h =", h)

g = f*h
print("\ng = f * h =", g)


# Ouptuts:
# f = -6*xbar^10 + xbar^8 + 10*xbar^7 - 5*xbar^6 + xbar^5 + 3*xbar^4 - 6*xbar^3 + 7*xbar^2 + 7*xbar + 9
# h = xbar^10 + 5*xbar^9 - 9*xbar^8 - 7*xbar^7 + 2*xbar^6 - 5*xbar^5 + 7*xbar^4 - 3*xbar^3 + 4*xbar^2 - 7*xbar - 6
# 
# g = f * h = -xbar^10 - 45*xbar^9 - 194*xbar^8 - 101*xbar^7 + 142*xbar^6 - 44*xbar^5 + 3*xbar^4 - 69*xbar^3 + 13*xbar^2 - 239*xbar + 157

呼叫 Matrix 類別，建構上面的 H 矩陣，並使用他內建的矩陣乘法：

f_coeff = f.list()
h_coeff = h.list()
g_coeff = g.list()


H = Matrix([[h_coeff[(i-j)%N] for i in range(N)] for j in range(N)])
print(H)
F = Matrix([[f_coeff[i] for i in range(N)]])

print(F)
print("\n")
print(F*H)
print(g_coeff)

# Outputs:
# [-6 -7  4 -3  7 -5  2 -7 -9  5  1]
# [ 1 -6 -7  4 -3  7 -5  2 -7 -9  5]
# [ 5  1 -6 -7  4 -3  7 -5  2 -7 -9]
# [-9  5  1 -6 -7  4 -3  7 -5  2 -7]
# [-7 -9  5  1 -6 -7  4 -3  7 -5  2]
# [ 2 -7 -9  5  1 -6 -7  4 -3  7 -5]
# [-5  2 -7 -9  5  1 -6 -7  4 -3  7]
# [ 7 -5  2 -7 -9  5  1 -6 -7  4 -3]
# [-3  7 -5  2 -7 -9  5  1 -6 -7  4]
# [ 4 -3  7 -5  2 -7 -9  5  1 -6 -7]
# [-7  4 -3  7 -5  2 -7 -9  5  1 -6]
# [ 9  7  7 -6  3  1 -5 10  1  0 -6]
# 
# [ 157 -239   13  -69    3  -44  142 -101 -194  -45   -1]
# [157, -239, 13, -69, 3, -44, 142, -101, -194, -45, -1]

可以發現，兩個結果是一樣的，所以我們已驗證這個等式的正確性。

將 f(x) 與 g(x) 寫成短向量：

先做成向量

首先，因為 f(x) 與 g(x) 應滿足

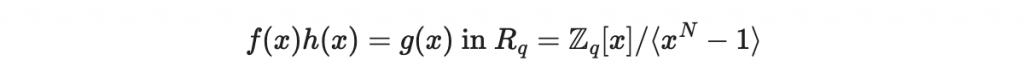
所以我們可以改寫為

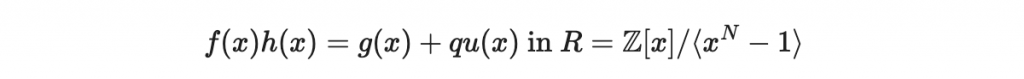
u(x) 是某個在 R 裡面的多項式。

因此我們可以故技重施：

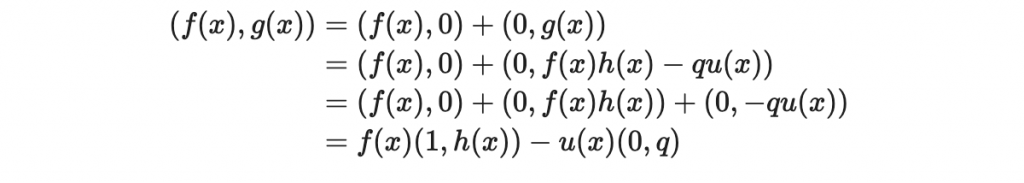
現在我們嘗試將這個寫成「係數的向量」：首先對付 f(x)(1, h(x))

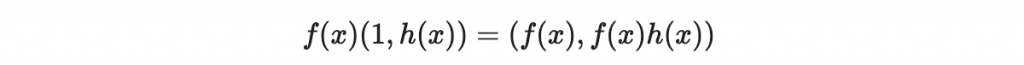
而左邊可以寫為以下矩陣乘法

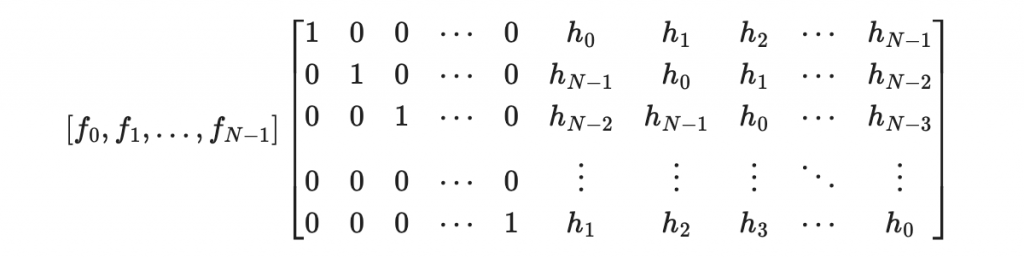
我們把它記作

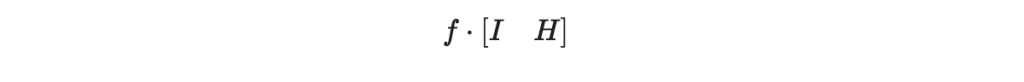
接著對付 -u(x)(0, q)

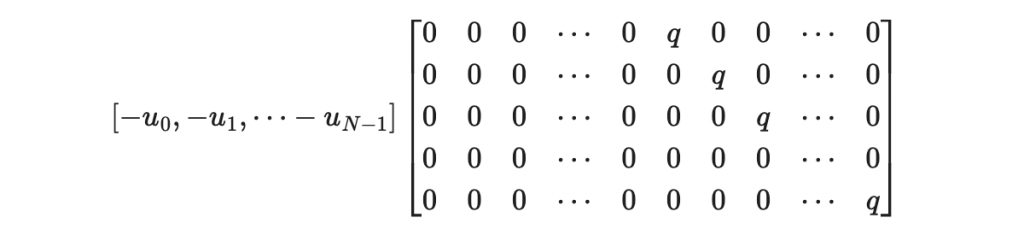
我們把它記作

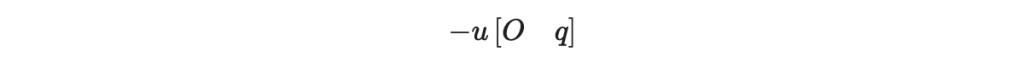
因此，

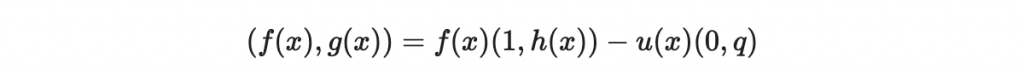
可以寫為

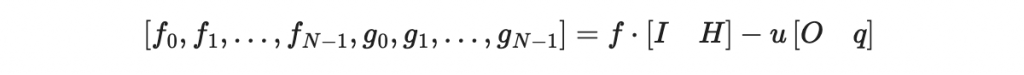
或整更簡潔地

短向量問題

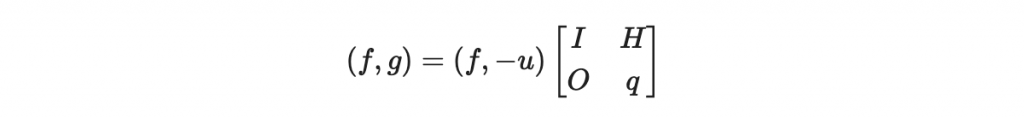
好的，接著我們來分析這個矩陣方程式

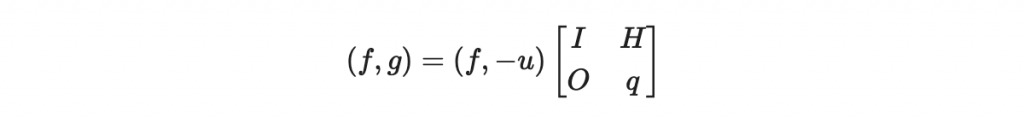
左手邊是一個 2N 維度的向量，我們希望他越小越好。

右手邊可以看成是矩陣

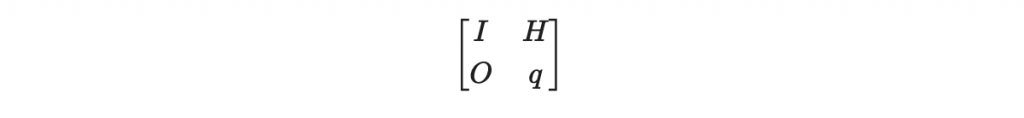
其行向量的整係數 (f_0, ..., f_N-1, -u_0, ..., -u_N-1) 線性組合

引此我們在做的其實是決定好整係數

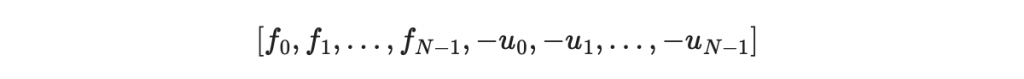
好讓他的結果向量

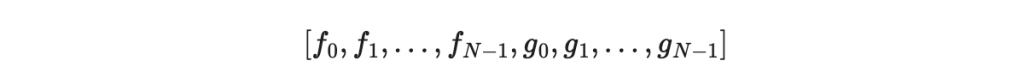
儘量的小。

恭喜，這就是標準的晶格短向量問題。

明天是第九天，是晶格密碼學的最後一篇，我們會帶過相關的攻擊方式，並介紹一些其他的加密標準。

Takeaway

• 多項式乘法可以用矩陣來寫，除了可以用代數證明以外，我們也可以寫程式來確認該等式。
• NTRU 密碼系統的解碼正確性依賴於參與其中的多項式的係數夠小
• 承上，也因此我們可以把尋找 f(x) 與 g(x) 的過程看為「尋找短向量」